ECCCos from the Black Box
Faithful Model Explanations through Energy-Constrained Conformal Counterfactuals
Counterfactual explanations offer an intuitive and straightforward way to explain opaque machine learning (ML) models. They work under the premise of perturbing inputs to achieve a desired change in the predicted output. There are typically many ways to achieve this, in other words, many different counterfactuals may yield the same desired outcome. A key challenge for researchers has therefore been to, firstly, define certain desirable characteristics of counterfactual explanations and, secondly, come up with efficient ways to achieve them.
One of the most important and studied characteristics of counterfactual explanations is ‘plausibility’: explanations should look realistic to humans. Plausibility is positively associated with actionability, robustness (Artelt et al. 2021) and causal validity (Mahajan, Tan, and Sharma 2020). To achieve plausibility, many existing approaches rely on surrogate models. This is straightforward but it also convolutes things further: it essentially reallocates the task of learning plausible explanations for the data from the model itself to the surrogate.
In our AAAI 2024 paper, Faithful Model Explanations through Energy-Constrained Conformal Counterfactuals (ECCCo), we propose that we should not only look for explanations that please us but rather focus on generating counterfactuals that faithfully explain model behavior. It turns out that we can achieve both faithfulness and plausibility by relying solely on the model itself, leveraging recent advances in energy-based modelling and conformal prediction. We support this claim through extensive empirical studies and believe that ECCCo opens avenues for researchers and practitioners seeking tools to better distinguish trustworthy from unreliable models.
This is a companion post to our recent AAAI 2024 paper co-authored with Mojtaba Farmanbar, Arie van Deursen and Cynthia C. S. Liem1. The paper is a more formal and detailed treatment of the topic and is available here. This post is intentionally free of technical details, maths or code. It is meant to provide a high-level overview of the paper.
Pick your Poison
There are two main philosophical debates in the field of Explainable AI (XAI). The first one centers around the role of explainability in AI: do we even need explanations and if so, why? Some have argued that we need not care about explaining models as long as they produce reliable outcomes (Robbins 2019). Humans have not shied away from this in other domains either: doctors, for example, have prescribed aspirin for decades without understanding why it is a reliable drug for pain relief (London 2019). While this reasoning may rightfully apply in some cases, experiments conducted by my colleagues at TU Delft have shown that humans do not make better decisions if aided by a reliable and yet opaque model (He, Buijsman, and Gadiraju 2023). In these studies, subjects tended to ignore the AI model indicating that they did not trust its decisions. Beyond this, explainability comes with numerous advantages such as accountability, control, contestability and the potential for uncovering causal relationships.
If we can blindly rely on the decisions made by an AI, why should we even bother to come up with explanations? I must confess I had never even seriously considered this as an option until attending Stefan Buijsman’s recent talk at a Delft Design for Values workshop, which inspired the previous paragraph. As a philosopher and AI ethicist at TU Delft, some of Stefan’s most recent research investigates causal human-in-the-loop explanations for AI models (Biswas et al. 2022). I do not think that he adheres to the view that we should simply trust AI models blindly. In fact, he and his colleagues have shown that most humans do not tend to simply trust AI models even if they have been assured about their reliability (He, Buijsman, and Gadiraju 2023).
Still, the question of why we even bother is an interesting challenge, especially considering that the field of XAI has so far struggled to produce satisfactory and robust results with meaningful real-world impact. Numerous studies related to He, Buijsman, and Gadiraju (2023) have shown that explanations for AI models either fail to help users or even mislead them (Mittelstadt, Russell, and Wachter 2019; Alufaisan et al. 2021; Lakkaraju and Bastani 2020). It seems that neither blind trust nor explanations are a silver bullet.
So, have our efforts toward explainable AI been in vain? Should we simply stop explaining black-box models altogether as proposed by Rudin (2019)? Having worked in this field for a little over 2 years now, I have personally grown more and more skeptical of certain trends I have observed. In particular, I think that the community has focused too much on finding explanations that please us independent of the model itself (ideally model-agnostic, really!). This is a bit like applying a band-aid to a wound without first cleaning it. At best, plausible explanations for untrustworthy models provide a false sense of security. At worst, they can be used to manipulate and deceive. The AAAI paper presented in this post is very much born out of skepticism about this trend.
Nonetheless, I do not think all hope is lost for XAI. I strongly believe that there is a need for algorithmic recourse as long as we continue to deploy black-box models for automated decision-making. While I am fully supportive of the idea that we should always strive to use models that are as interpretable as possible (Rudin 2019), I also think that there are cases where this is not feasible or it is simply too convenient to use a black-box model instead. The aspirin example mentioned above is a striking example of this. But it is easy enough to stretch that example further to illustrate why explainability is important. What if the use of aspirin was prohibited for a small minority of people and there was a reliable, opaque model to decide who belonged to that group? If you were part of that group, would you not want to know why? Why should you have to endure headaches for the rest of your life while others do not?
In summary, I think that—like it or not—we do need to bother.
The second major debate is about what constitutes a good explanation, because, crucially, explanations are not unique: was your headache cured by the aspirin you took before going to sleep or sleep itself? Or a combination of both? This multiplicity of explanations arises almost naturally in the context of counterfactual explanations. Unless the combination of input features for which the model predicts the target class or value is unique, there is always more than one possible explanation. As an illustrative example, consider the counterfactuals presented in Figure 1. All of these are valid explanations for turning a ‘nine’ into ‘seven’ according to the underlying classifier (a simple multi-layer perceptron). They are all valid in the sense the model predicts the target label with high probability in each case. The troubling part is that even though all of the generated counterfactuals provide valid explanations for why the model predicts ‘seven’ instead of ‘nine’, they all look very different.
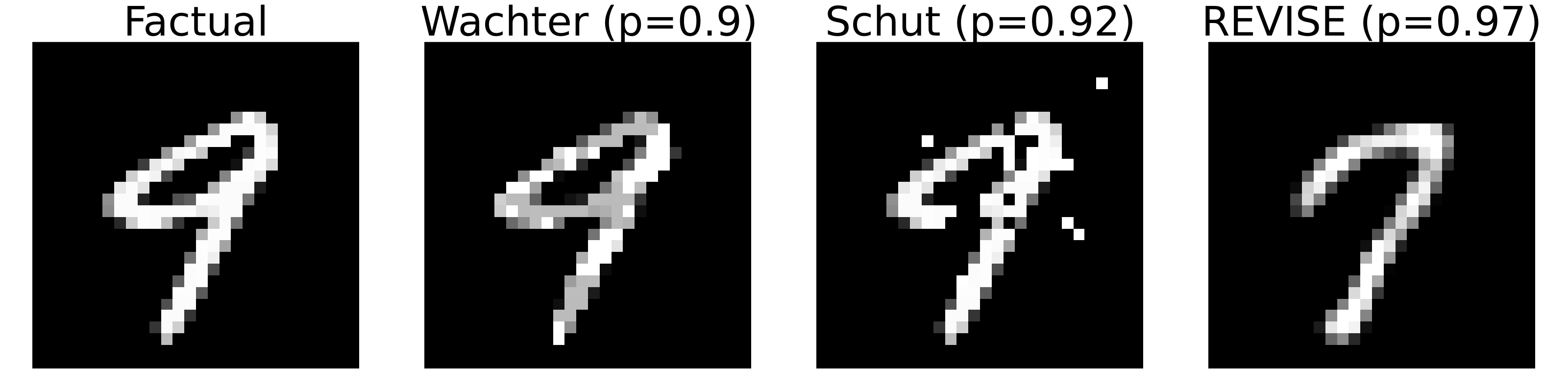
So, which explanations do we trust most? Which one would you choose to present to an audience to explain how the classifier decides which digit to predict? Arguably, the counterfactual on the far right looks most like a ‘seven’, so I am willing to bet that most people would simply choose that one. It is valid after all and it looks plausible, while the other two counterfactuals might just lead to awkward questions from more interrogative audience members. In any case, I mentioned earlier that more plausible explanations tend to also be more actionable and robust, so this seems fair game. The counterfactual produced by REVISE (Joshi et al. 2019) is the poison we will pick—dump the rest and move on. Plausibility is all we need!2
I am exaggerating but I do think that as a community of researchers studying counterfactual explanations, we have become so absorbed by the pursuit of a few desiderata that we have forgotten that ultimately we are in the business of explaining models. Our primary mandate is to design tools that help us understand why models predict certain outcomes. How useful is a plausible, actionable, sparse, causally valid explanation in gaining that understanding, if there exist a whole bunch of other valid explanations that do not meet these desiderata? Have we significantly improved our understanding of the underlying classifier in Figure 1 and therefore established a higher degree of trust in the model, simply because we have found a plausible counterfactual?
In my mind, we most certainly have not. I would argue that the existence of a valid and plausible explanation merely serves to reassure us that the model is not entirely ignorant about meaningful representations in the data. But as long as entirely implausible counterfactuals are also valid according to the model, selectively relying only on the subset of plausible counterfactuals may lead to a wrong sense of trust in untrustworthy models. That is why in our paper we argue that explanations should be faithful first, and plausible second.
Faithful First, Plausible Second
To navigate the interplay between faithfulness and plausibility, we propose a way to generate counterfactuals that are consistent with what the model has learned about the data. In doing so, we can also achieve plausibility but only in case the model has learned something meaningful.
Faithful Counterfactuals
When inquiring about what is “consistent with what the model has learned about the data”, we are essentially asking about the model’s posterior conditional distribution of the input data given the target output. It turns out that we can approximate that distribution using ideas relevant to energy-based modelling. In particular, we can use something called Stochastic Gradient Langevin Dynamics (SGLD) to sample from the model’s posterior conditional distribution (Welling and Teh 2011).
Without going into too much detail here, the idea is to use the model’s energy function to guide the sampling process. The energy function is a scalar function that assigns a value to each possible configuration of the input data. The lower the energy, the higher the likelihood corresponding to the configuration. This is a powerful tool: Grathwohl et al. (2020), for example, use SGLD in this fashion to train hybrid models—joint-energy models (JEM)—that are trained to both classify and generate data.
Figure 2 illustrates this concept. It shows samples (yellow stars) drawn from the posterior of a simple JEM trained on linearly separable data. The contour shows the kernel density estimate (KDE) for the learned conditional distribution. Although it seems that the posterior is too sharp in this case, the learned conditional distribution is overall consistent with the data (at least the mode is).
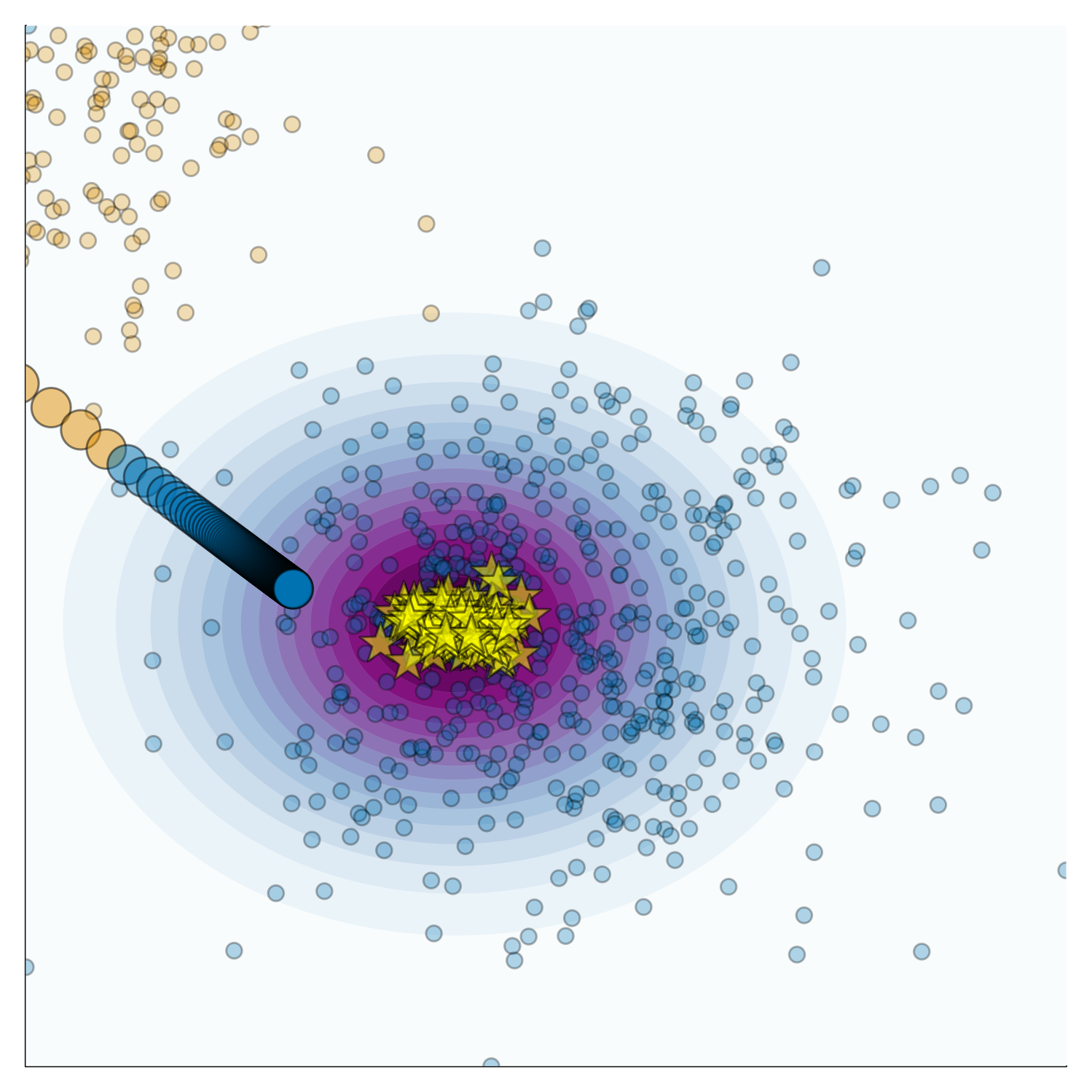
Also shown in Figure 2 is a single counterfactual path from the orange to the blue class. I have relied on the baseline approach proposed in Wachter, Mittelstadt, and Russell (2017) here using only a small penalty for the distance between the counterfactual and the original input. A truly faithful counterfactual, as we define it in our paper, would be one that we could expect to sample from the learned conditional distribution (with high probability)3. Based on this notion, we would not characterize the counterfactual in Figure 2 as faithful, but it also is not too far off.
It is easy to see how other desiderata may conflict with faithfulness. If I had penalized the distance between the counterfactual and the original input more, for example, then the counterfactual would have been less costly but also less faithful. This is the sort of trade-off between different desiderata that we always need to navigate carefully in the context of counterfactual explanations. As we will see next, the same also applies to plausibility but in a different way.
Plausible Counterfactuals
If you have followed the discussion so far, then you have already understood the trickiest concept in our paper. Plausibility can be defined much like we have done for faithfulness, but it is a bit more straightforward. In our paper, we broadly define plausible counterfactals as those that are indistinguishable from the observed data in the target domain. We already touched on this above when discussing the counterfactual images in Figure 1.
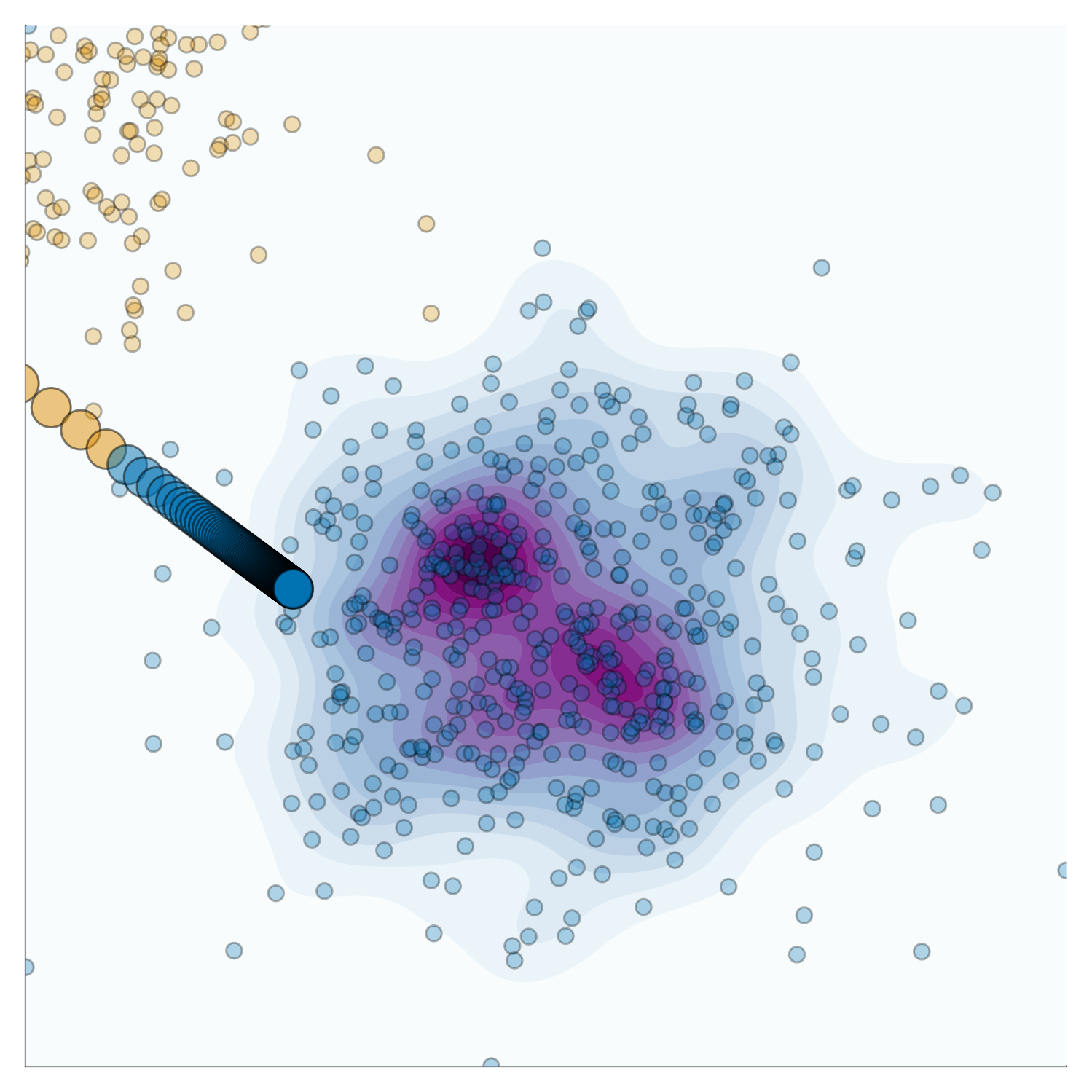
Figure 3 illustrates the same concept for the same JEM as in Figure 2. The KDE in Figure 3 shows the conditional distribution based on the observed data. The counterfactual path is the same as in Figure 2. The counterfactual is plausible in this case since it is not easily distinguishable from the observed data in the target domain.
Looking at both Figure 2 and Figure 3, it becomes evident why the interplay between faithfulness and plausibility need not necessary be a trade-off. In this case, the counterfactual is neither terribly unfaithful nor implausible. This is because the learned conditional distribution is broadly consistent with the observed distribution of the data.
Our approach: ECCCo
Now that we have covered the two major concepts in our paper, we can move on to our proposed approach for generating faithful counterfactuals: ECCCo. As the title of the paper suggests, ECCCo is an acronym for Energy-Constrained Conformal Counterfactuals. We leverage ideas from energy-based modelling and conformal prediction, in particular from Grathwohl et al. (2020) and Stutz et al. (2022), respectively. Our proposed counterfactual generation process involves little to no overhead and is broadly applicable to any model that can be trained using stochastic gradient descent. Technical details can be found in the paper. For now, let us focus on the high-level idea.
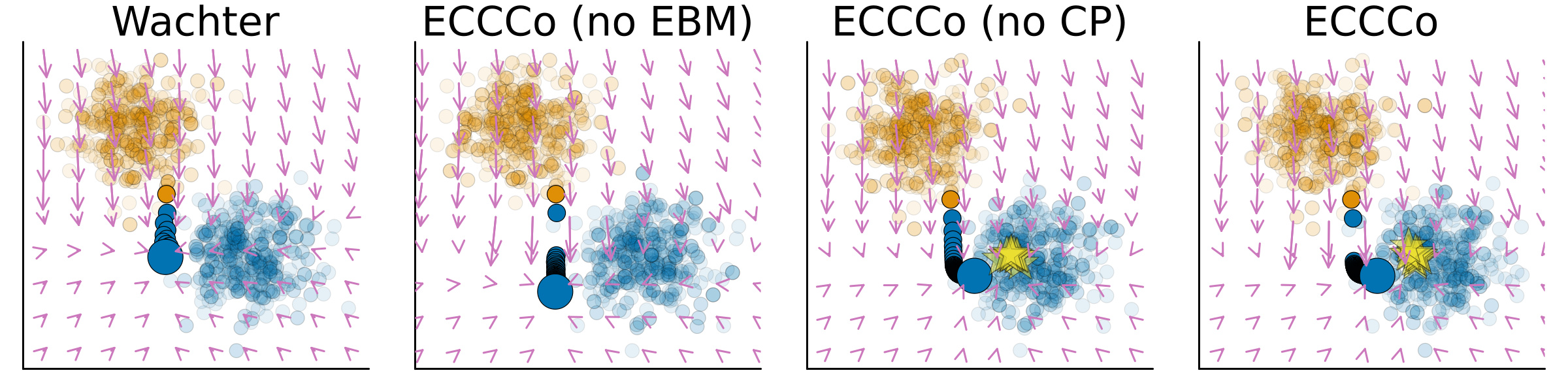
Figure 4 compares the counterfactual path generated by Wachter (Wachter, Mittelstadt, and Russell 2017) to those generated by ECCCo, where we use ablation to remove the energy constraint—ECCCo (no EBM)—and the conformal prediction component—ECCCo (no CP). In this case, the counterfactual generated by Wachter is neither faithful nor plausible. It does, however, minimize the distance between the counterfactual and the original input.
The counterfactual generated by ECCCo (no EBM) is deeper inside the blue class and has avoided points near the decision boundary on its path to its final destination. This is because ECCCo (no EBM) involves a penalty term for predictive uncertainty, which is high near the decision boundary. Intuitively, we would expect that avoiding regions of high predictive uncertainty in our counterfactual search should help with plausibility (Schut et al. 2021). In this particular case, the final counterfactual is neither more faithful nor more plausible than the one generated by Wachter, but in our experiments we have generally found that penalizing predictive uncertainty alone can help to generate more faithful and plausible counterfactuals.
The counterfactual generated by ECCCo (no CP) is more faithful than the one generated by Wachter and ECCCo (no EBM). This is because the energy constraint induces counterfactuals that are more consistent with the learned conditional distribution (as in Figure 2). Since the model has learned something meaningful about the data, the counterfactual is also more plausible than the one generated by Wachter and ECCCo (no EBM) in this case.
The counterfactual path generated by ECCCo combines benefits from both the energy constraint and the conformal prediction component. It avoids regions of high predictive uncertainty and ends up at a point that is consistent with the learned conditional distribution.
Results
In the paper, we present results from extensive empirical studies involving eight datasets from different domains and a variety of models. We compare ECCCo to state-of-the-art counterfactual generators and show that it consistently outperforms these in terms of faithfulness and often achieves the highest degrees of plausibility. Here we will highlight some visual results from the MNIST dataset.
Figure 5 shows counterfactuals generated using different counterfactual generators on the MNIST dataset. In this example, the goal is to generate a counterfactual in class ‘five’ for the factual ‘three’. The ECCCo+ generator is a variant of ECCCo that performs gradient search in the space spanned by the first few principal components. This reduces computational costs and often helps with plausibility, sometimes at a small cost of faithfulness. The counterfactuals generated by ECCCo and ECCCo+ are visibly more plausible than those generated by the other generators. In the paper, we quantify this using custom metrics for plausibility and faithfulness that we propose.

We also find that the counterfactuals generated by ECCCo are more faithful in this case. The underlying model is a LeNet-5 convolutional neural network (LeCun et al. 1998). Even today, convolutional neural networks are still among the most popular neural network architectures for image classification. Contrary to the simple multi-layer perceptron (MLP) used in Figure 1, the LeNet-5 model is a bit more complex and it is not surprising that it has distilled more meaningful representations in the data.
More generally, we find that ECCCo is particularly effective at producing plausible counterfactuals for models that we would expect to have learned more meaningful representations of the data. This is consistent with our claim that ECCCo generates faithful counterfactuals. Figure 5 shows the results for applying ECCCo to the same factual ‘nine’ as in Figure 1 for different models from left to right and top to bottom: (a) an MLP, (b) a deep ensemble of MLPs, (c) a JEM, and, (d) a deep ensemble of JEMs. The plausibility of the generated counterfactual gradually improves from left to right and top to bottom as we get more rigorous about model complexity and training: deep ensembling can help to capture predictive uncertainty and joint-energy modelling is explicitly concerned with learning meaningful representations in the data.

We would argue that in general, this is a desirable property of a counterfactual explainer, because it helps to distinguish trustworthy from unreliable models. The generated counterfactual for the MLP in (a) in Figure 6 is grainy and altogether not very plausible. But this is precisely because the MLP is not very trustworthy: it is sensitive to input perturbations that are not meaningful. We think that explanations should reflect these kinds of shortcomings of models instead of hiding them.
Conclusion
This post has provided a brief and accessible overview of our AAAI 2024 paper that introduces ECCCo: a new way to generate faithful model explanations through energy-constrained conformal counterfactuals. The post has covered some of the main points from the paper:
- We have argued that explanations should be faithful first, and plausible second.
- We show that ECCCo consistently outperforms state-of-the-art counterfactual generators in terms of faithfulness and often achieves the highest degrees of plausibility.
- We believe that ECCCo opens avenues for researchers and practitioners seeking tools to better distinguish trustworthy from unreliable models.
Software
The code for the experiments in the paper is available on GitHub: https://github.com/pat-alt/ECCCo.jl. The repo contains job scripts for running the experiments on a SLURM cluster, as well as the source code for the ECCCo package. The package is written in Julia and built on top of CounterfactualExplanations.jl, which will eventually absorb the functionality of ECCCo.
References
Footnotes
Besides my co-authors, I also want to thank the anonymous reviewers at both NeurIPS and AAAI for their valuable feedback as well as Nico Potyka and Francesco Leofante for interesting discussions on the topic.↩︎
Considering how much I have cited Joshi et al. (2019) in the past, I think it should go without saying that I very much like this paper, despite taking a critical stance on it here.↩︎
I have had an interesting chat with Nico Potyka and Francesco Leofante, recently, where they rightly pointed out that this definition of faithfulness needs to be refined. In particular, one might wonder what constitutes a ‘high probability’ in this context. I think this is a very valid point and I am looking forward to discussing this further with them.↩︎
Citation
@online{altmeyer2024,
author = {Altmeyer, Patrick},
title = {ECCCos from the {Black} {Box}},
date = {2024-02-08},
url = {https://www.patalt.org/blog/posts/eccco/},
langid = {en}
}